Definindo bielas em blocos de fundação

No dimensionamento de blocos de fundação pelo método de bielas e tirantes, é necessário conhecer o ângulo vertical e o ângulo em planta do eixo das bielas. Assim, podemos obter as componentes de força para verificar as tensões no concreto e também calcular as armaduras dos tirantes.

O modelo mais simples de definir o eixo da biela é traçar uma linha partindo do centro do pilar até o centro da estaca.

Considerar que o eixo da biela parte do centro do pilar não é muito preciso, principalmente quando temos pilares de grandes dimensões.

Neste artigo, quero explicar um modelo simples e bastante utilizado para definir o eixo das bielas e como pode ser generalizado para qualquer número de estacas: o modelo das isoáreas.

Talvez você já tenha visto uma figura parecida com essa: um corte de um bloco com duas bielas partindo do pilar e chegando nas estacas.

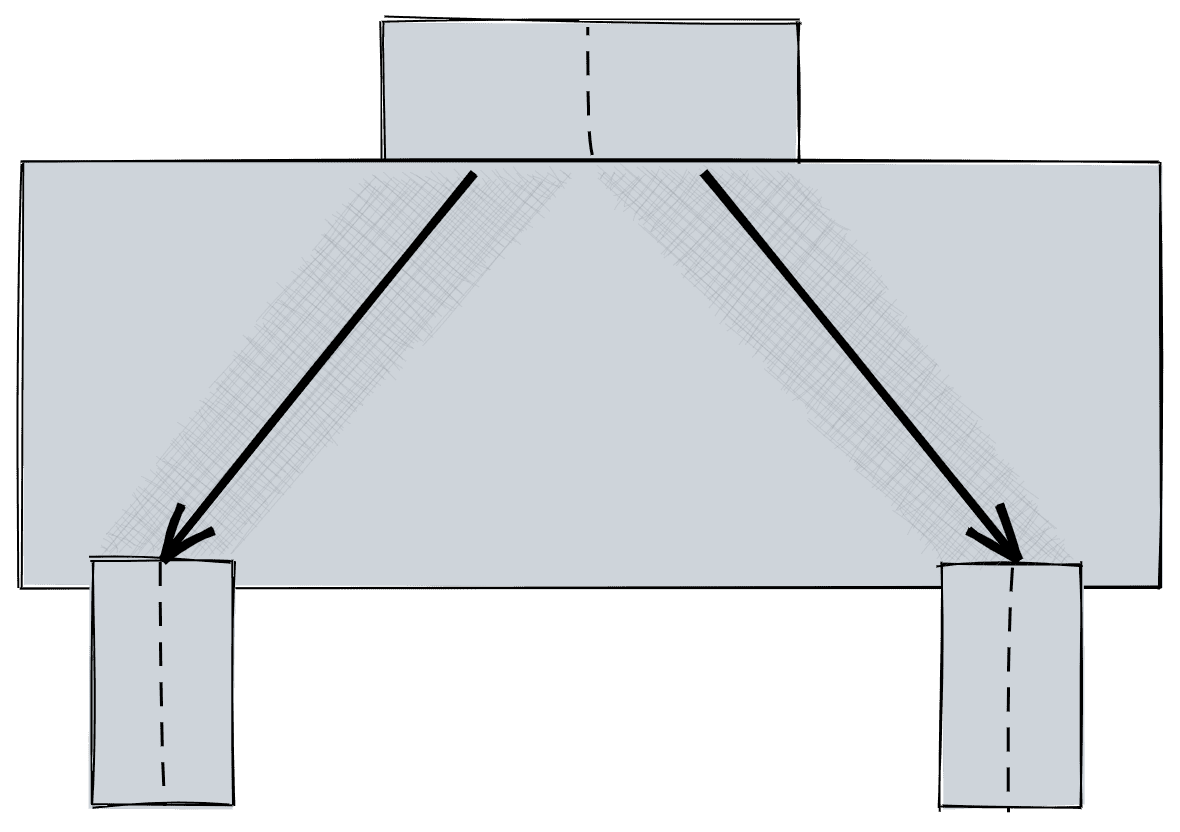
Talvez você também já tenha reparado que normalmente as bielas não partem do centro do pilar, nesse caso simples, é intuitivo dividir o pilar em dois e fazer a biela partindo do centro de cada metade.

(Neste artigo, para desenrolar a linguagem, falo simplesmente “biela” para me referir ao “eixo” da biela).

Bom, esse já é o modelo das isoáreas. Quero ir um pouco mais fundo e mostrar como ele pode ser utilizado em blocos com qualquer número e disposição de estacas. Mas primeiro, por que normalmente não consideramos que as bielas partem do centro do pilar?

Consequências de considerar as bielas partindo do centro do pilar

Vamos traçar as bielas de um bloco com um pilar relativamente pequeno.

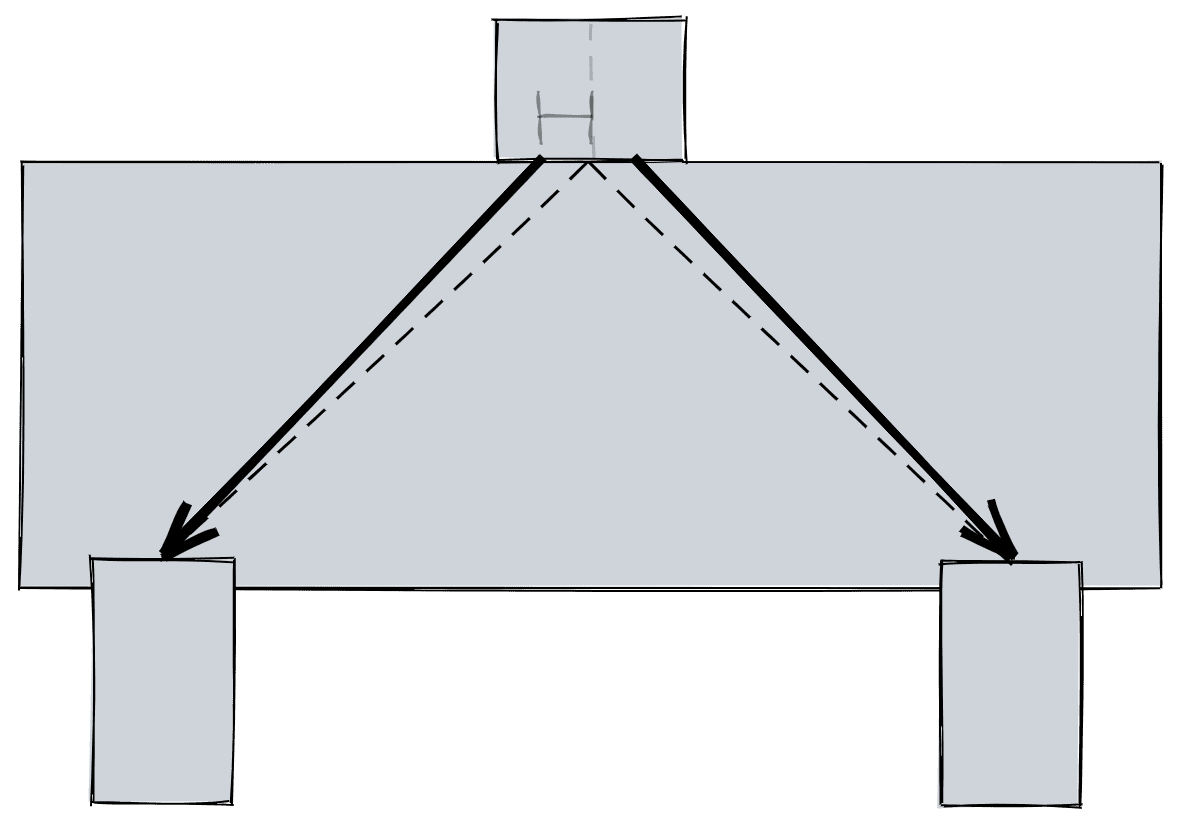
Nesse caso, a biela que parte de umas das metades é bem próxima da que parte do centro do pilar. Mas é fácil perceber que, quanto maior o pilar, maior será essa diferença. Vamos ver um outro exemplo.

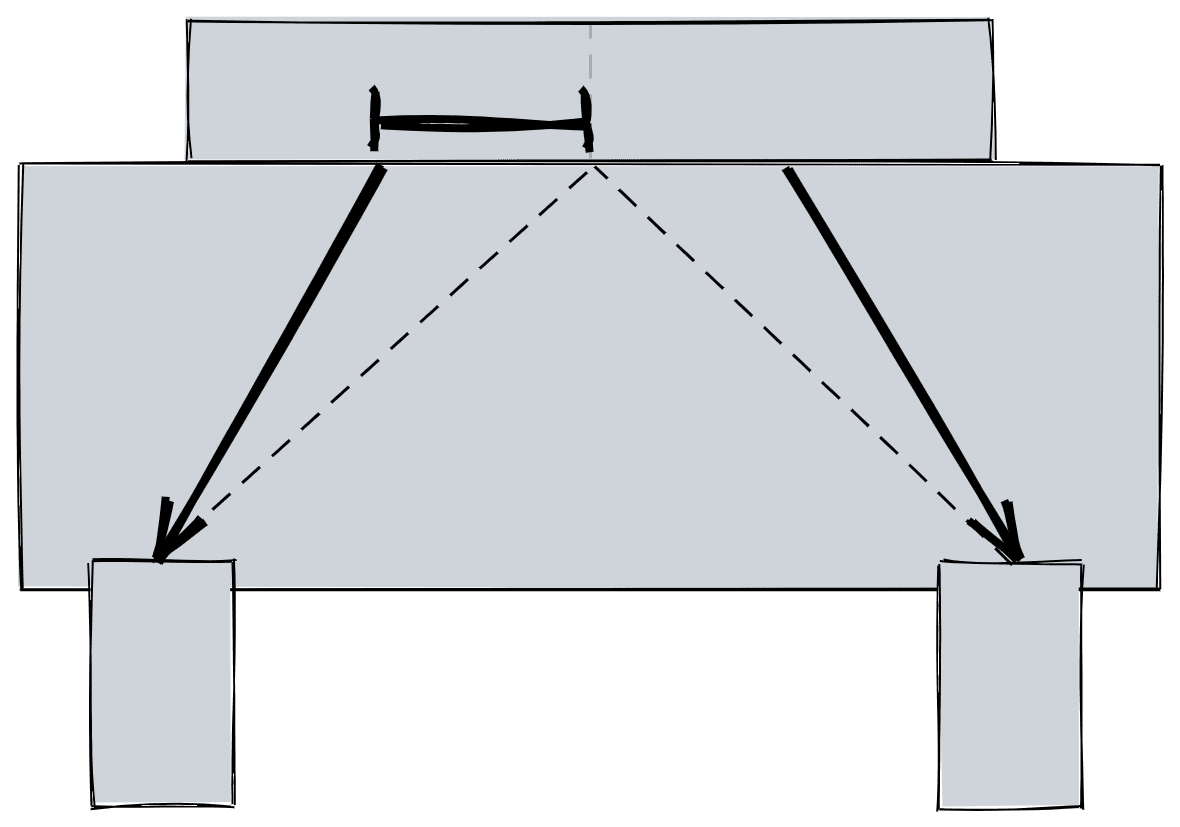
No modelo em que a biela parte do centro do pilar, ela percorre uma distância maior até chegar na estaca e será mais abatida do que deveria ser. Assim, temos duas possíveis consequências:

• Será necessário aumentar a altura do bloco para respeitar o critério de ângulo mínimo da biela;
• Se a biela é mais abatida do que a “real”, estaremos superdimensionando a armadura dos tirantes.

Portanto, temos uma implicação prática do modelo considerado, já que uma maior altura do bloco ou quantidade de armadura tem impactos no custo de execução.

O modelo das isoáreas

A ideia do modelo é dividir o pilar e associar cada divisão a uma determinada estaca, dessa forma, a biela parte do centro da divisão ao invés do centro do pilar. O número de divisões do pilar é igual ao número de estacas.

Em blocos de poucas estacas, a divisão do pilar é de certa forma intuitiva. Para duas estacas, dividimos o pilar em duas áreas de onde partem as bielas. O mesmo vale para quatro estacas, mas, desta vez, dividimos o pilar em quatro.

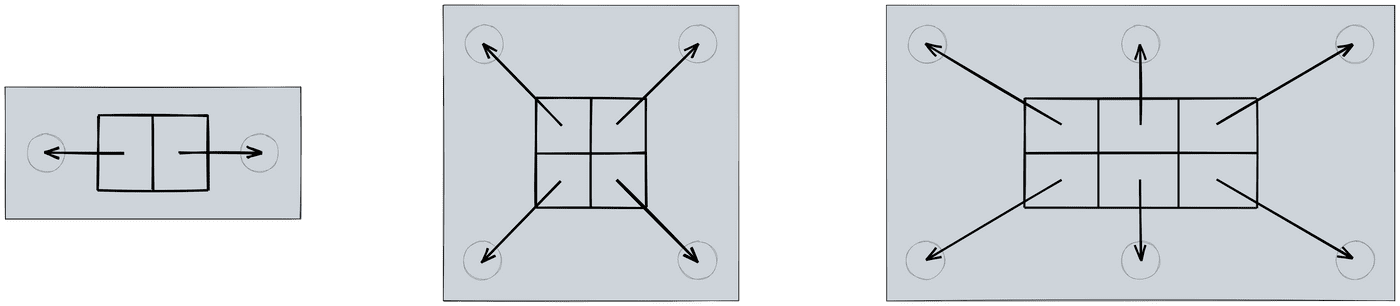
Conforme o número de estacas aumenta e o arranjo fica mais complexo, já não é tão óbvio como fazer essa divisão. Como dividir o pilar para um bloco assim?

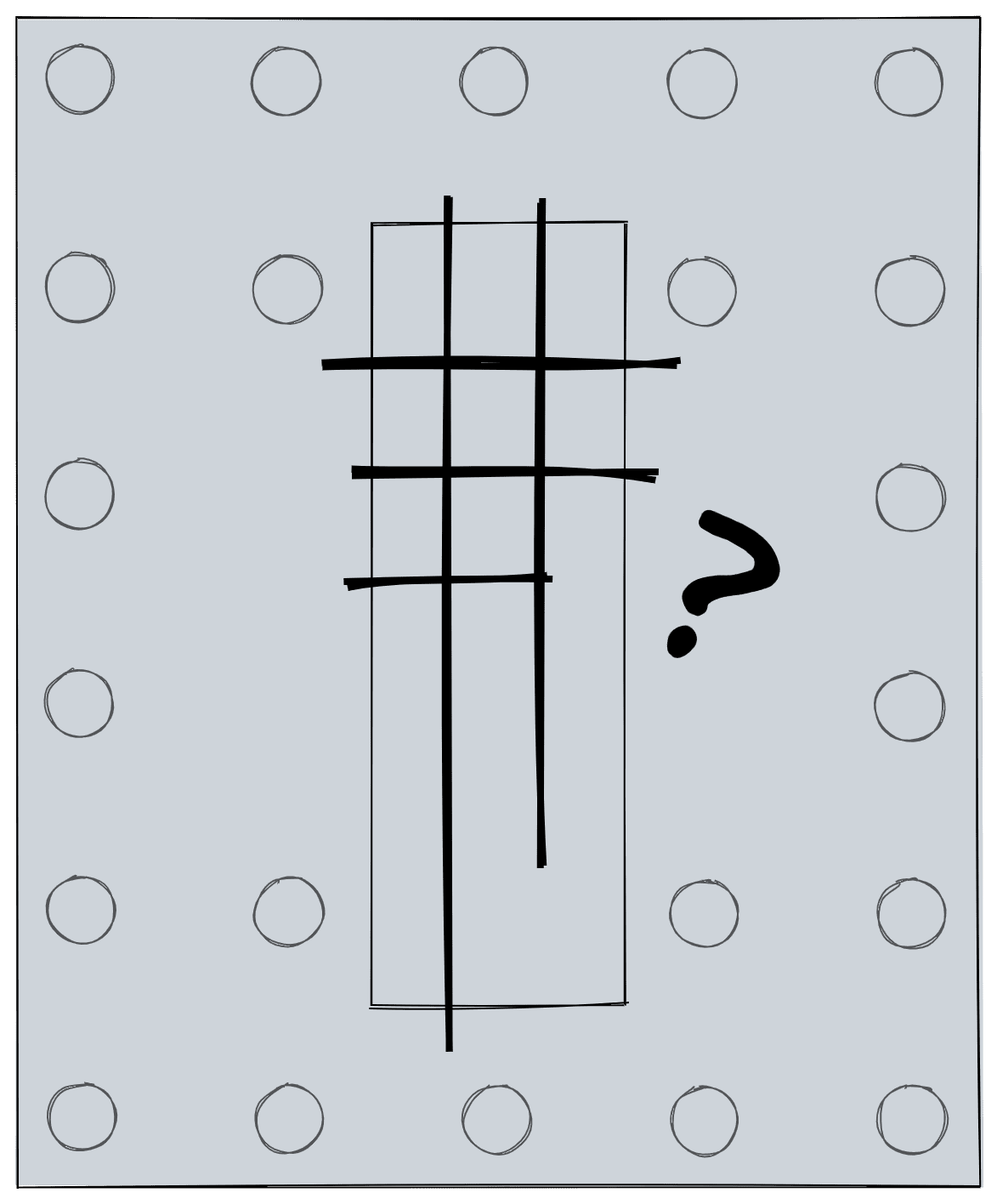
Um dos primeiros projetos que participei depois da graduação foi dimensionar blocos de fundação para algumas pontes ferroviárias. As cargas eram pesadas para a capacidade das estacas, então, os blocos quase sempre tinham mais de 20 estacas. Esse exemplo que acabei de mostrar foi um bloco real que eu tinha que dimensionar.

O meu chefe me ensinou um jeito. A sacada era simplificar o problema e admitir que a área de todas as divisões eram iguais. Em seguida, era feito um “mapeamento” entre a disposição das estacas e as divisões do pilar. Por falta de um nome melhor, eu chamo esse modelo de modelo das isoáreas.

A divisão do pilar ficaria assim:

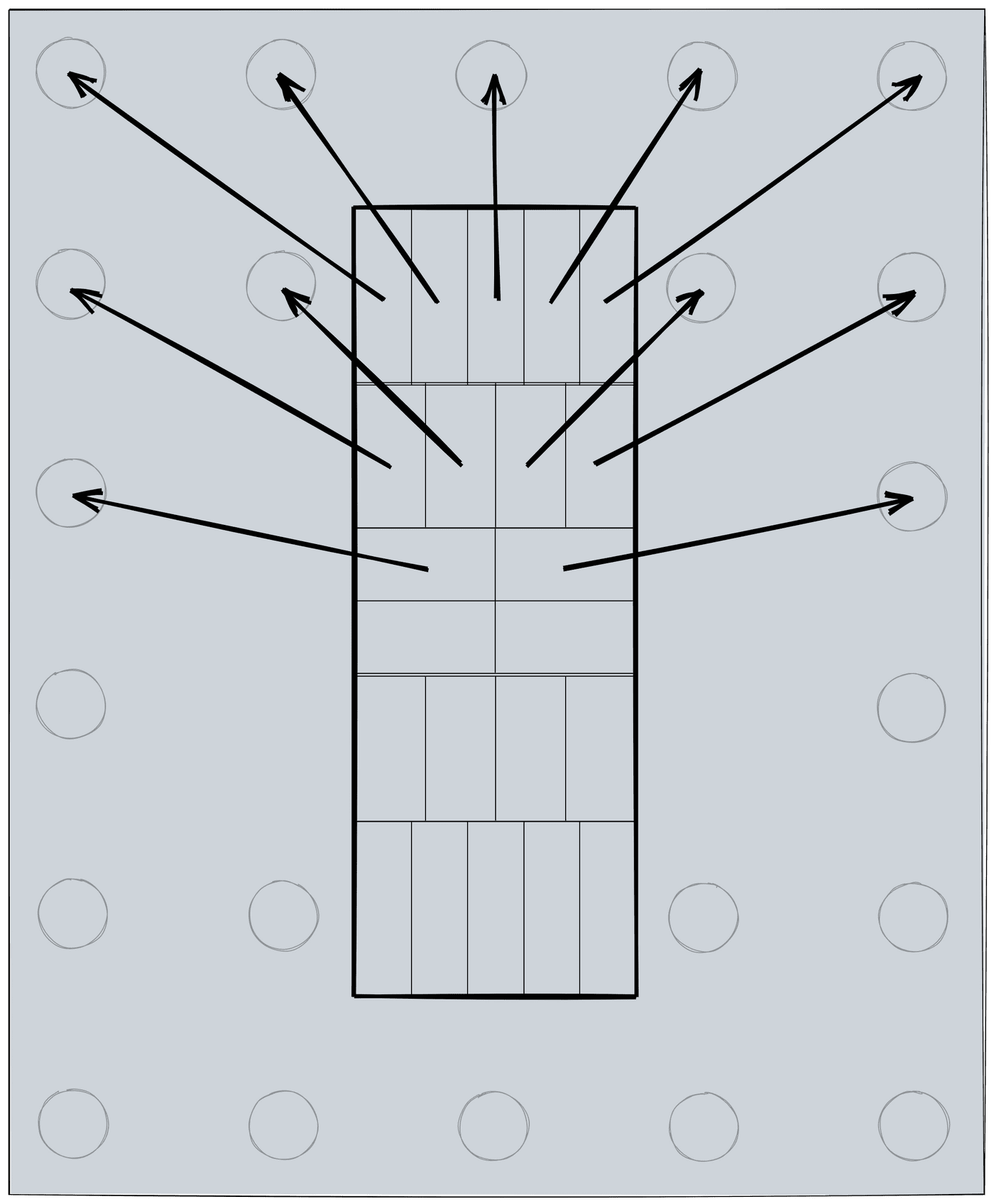
Para aplicar esse modelo, eu utilizava o bom e velho autoCAD. Eu desenhava o bloco com as suas estacas e começava a dividir o pilar em “retângulos” e ligar o centro de cada um deles a uma estaca com uma linha. Depois, eu utilizava a ferramenta de medir ângulo do autoCAD e “pronto”.

Mas se tem uma coisa que trabalhar com projeto ensina muito bem é: esteja preparado para mudanças. Não demorava muito para que alguma carga fosse alterada ou alguma premissa revisada.

Esse jeito de dividir o pilar “na mão” utilizando o autoCAD não era eficiente para lidar com mudanças frequentes. Então, comecei a pensar num jeito de automatizar esse processo utilizando uma planilha.

O que eu fiz foi pensar num jeito de “traduzir” esse processo manual num algoritmo. Ele ficou assim:

1. Calcular cada isoárea $(A)$ dividindo a área do pilar $(A_p)$ pelo número de estacas $(n)$. $A = A_p / n$;
2. Obter a quantidade de estacas em cada linha $(n_i)$;
3. Começando pela primeira linha de estacas, calcular a largura $l_x$ do retângulo dividindo o valor da isoárea pelo número de estacas na linha $(A/n_i)$;
4. Calcular a largura $l_y$ do retângulo dividindo $A/l_x$;
5. Dispor os retângulos lado a lado na primeira “linha” do pilar;
6. Repetir o processo para todas as linhas de estacas;
7. Ligar o centro de cada isoárea a sua respectiva estaca.

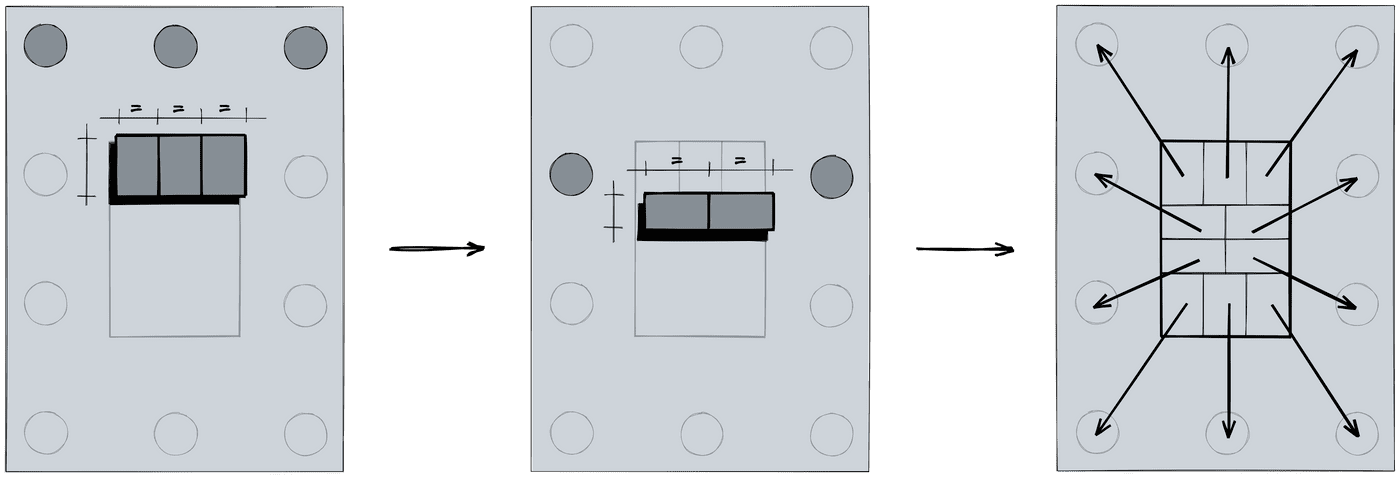
Escrevendo o algoritmo passo a passo parece ser mais complicado do que realmente é, mas é só uma questão de geometria. Essa é uma solução genérica e pode ser aplicada para qualquer número de estacas.

O exemplo interativo abaixo mostra como as bielas são definidas em diversos casos utilizando o modelo das isoáreas. Fique à vontade para brincar com os dados e criar o seu bloco selecionando a opção “Livre”.

Limitações do modelo e conclusão

Dividir o pilar em áreas iguais talvez seja o modo mais comum de resolver blocos de fundação rígidos. É um modelo simples e suficientemente preciso para a maioria dos casos.

Apesar da ideia de dividir o pilar ser genérica o suficiente, o algoritmo que apresentei parte da premissa de que o pilar tenha seção retangular cheia. Além disso, é claro que as bielas não se ajustam em retângulos perfeitos dentro do pilar, mas é melhor do que utilizar apenas o centro, o que, a grosso modo, ignoraria as dimensões do pilar.

O modelo também deve ser olhado com mais cuidado quando o bloco apresenta estacas tracionadas ou quando o pilar não se encontra totalmente comprimido.

Por fim, todo modelo é uma simplificação da realidade, mas nem sempre o mais elaborado é o melhor. Um modelo não linear de comportamento complexo pode ser necessário para algumas situações, mas muitas vezes, tudo o que precisamos é de algo simples que resolva o nosso problema com precisão suficiente. Cabe ao profissional conhecer as limitações do modelo, utilizá-lo quando for adequado e saber avaliar os seus resultados.

Neste artigo, foquei na divisão do pilar para definir a posição das bielas em planta. Num próximo artigo, falarei sobre alguns ajustes que podemos fazer em relação a posição vertical das bielas.