Como calcular as reações nas estacas de um bloco de fundação rígido

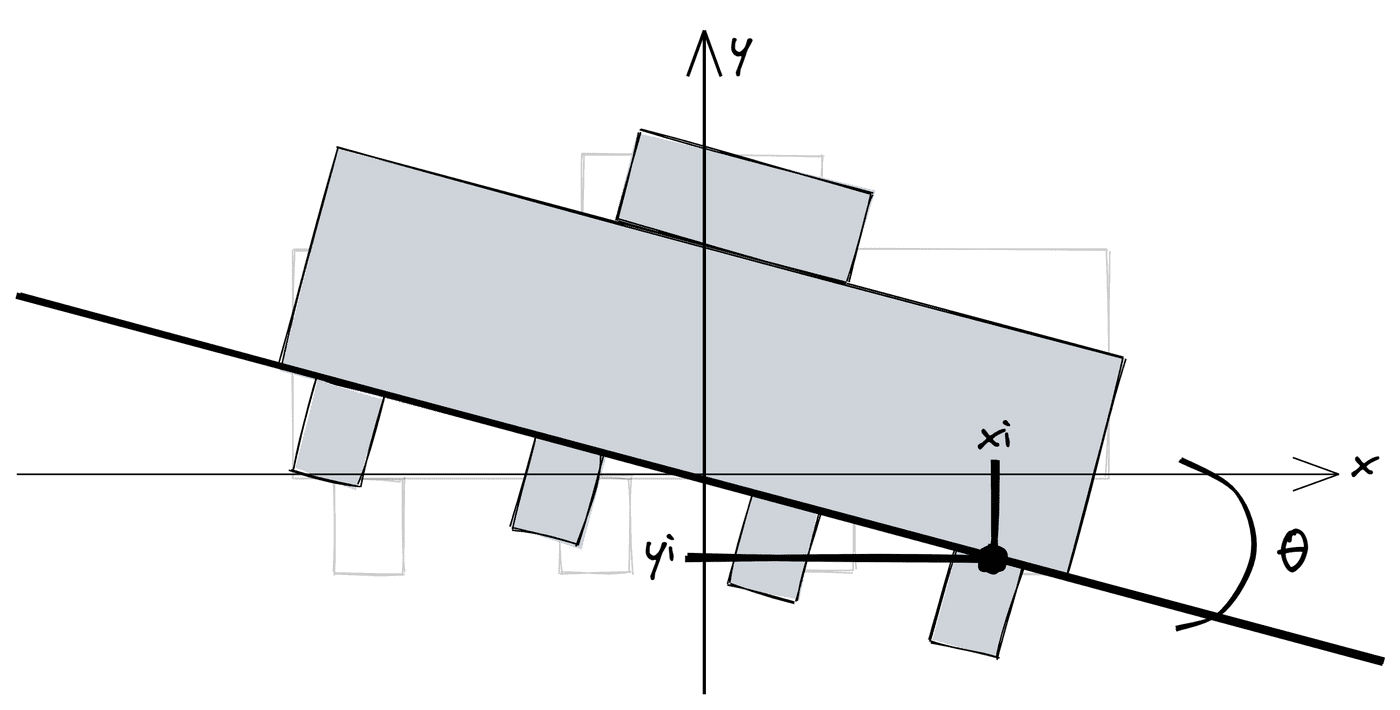
Este é o primeiro artigo de uma série que ensina o dimensionamento e detalhamento de blocos de fundação rígidos (também chamados de blocos sobre estacas ou blocos de coroamento) pelo método de bielas e tirantes (MBT).

É um assunto que tem muito o que explorar. Além de toda parte teórica e prática, eu também quero explicar como automatizar esse processo.

A ideia é ensinar um passo a passo que pode ser aplicado para um grande número de casos. Alguns passos podem parecer desnecessários para os blocos mais simples, mas serão úteis para blocos mais complexos.

Todo esse passo a passo parte da premissa de que o bloco de fundação seja rígido. Então, primeiro quero deixar claro o que isso significa.

Neste artigo vou focar no comportamento físico do bloco rígido e como, a partir disso, podemos deduzir uma equação para calcular as reações de um bloco com um número qualquer de estacas.

Considerar um bloco como rígido tem outras implicações além do cálculo das reações (por exemplo, no detalhamento da armadura). Estas outras questões serão explicadas em outro artigo.

O que é um corpo rígido

Um corpo rígido é aquele que não se deforma. Isso vale para qualquer estrutura, inclusive para blocos de fundação. Quando falamos que uma estrutura é rígida, estamos considerando que ela não se deforma.

Uma definição mais precisa é que ao escolher dois pontos de referência quaisquer em um corpo, a distância entre eles não muda ao aplicar uma força.

É interessante entender que rigidez é algo relativo, não existe um elemento 100% rígido. Tudo vai depender do quão rígido ele é em relação aos demais elementos que ele interage. É comum ouvir o termo “relação de rigidez” para descrever esse efeito.

Por curiosidade, podemos fazer um exercício de visualização para entender esse conceito.

Imagine uma régua de escritório, dessas de 30 cm. Dificilmente é um objeto que consideramos como rígido. Agora imagine que vamos apoiar essa régua numa superfície suficientemente mole, como uma espuma de barbear, e aplicar uma força no centro. Se estou conseguindo ser claro, podemos imaginar que ela vai simplesmente afundar, se deslocando verticalmente, mas sem deformar.

O próximo passo é apoiar esta régua numa superfície mais dura, na areia da praia, por exemplo. Aplicando uma força no meio, além de se deslocar verticalmente, ela também deforma. Os pontos do meio afundam mais que os da borda. Se escolhermos dois pontos de referência, vamos ver que a distância entre eles mudou, não podemos mais considerar o corpo como rígido. Portanto, um mesmo elemento pode ser considerado rígido ou não dependendo da condição em que se encontra.

A definição formal de corpo rígido tem uma aplicação prática. Vou começar pelo caso mais simples de todos: uma única força normal centrada, para entender como esse conceito pode ser utilizado no cálculo das reações.

Bloco de fundação rígido apenas com força normal centrada

Intuitivamente sabemos que para calcular a reação nas estacas quando temos apenas uma força normal centrada, basta dividir essa força pelo número de estacas.

Eu quero explicar de forma mais precisa o porquê isso é correto. Essa etapa pode parecer meio exagerada, mas vai ajudar a construir uma linha de raciocínio para casos mais complexos.

Imagine um bloco com 4 estacas numeradas de 1 a 4. O objetivo é calcular a reação $R_i$ de cada uma das estacas de índice $i$ ($R_1$, $R_2$, $R_3$ e $R_4$).

$R_i$ = reação vertical da estaca de índice $i$.

A Lei de Hooke diz que a força é proporcional ao deslocamento. Assim, para calcular a reação $R_i$, basta saber o quanto ela deslocou e multiplicar por uma constante (constante elástica $k$).

$R_i = y_i * k$

$y_i$ = deslocamento vertical da estaca $i$

Não conhecemos o valor da constante $k$, mas vamos considerar que ela seja igual para todas as estacas.

E é aqui que entra o comportamento de corpo rígido. Se o bloco for rígido, ele irá se deslocar apenas na vertical ao aplicar uma força centrada, assim como no exemplo da régua. Mais do que isso, também sabemos que o deslocamento de todas as estacas é o mesmo (aliás, não só das estacas, mas de qualquer outro ponto do bloco).

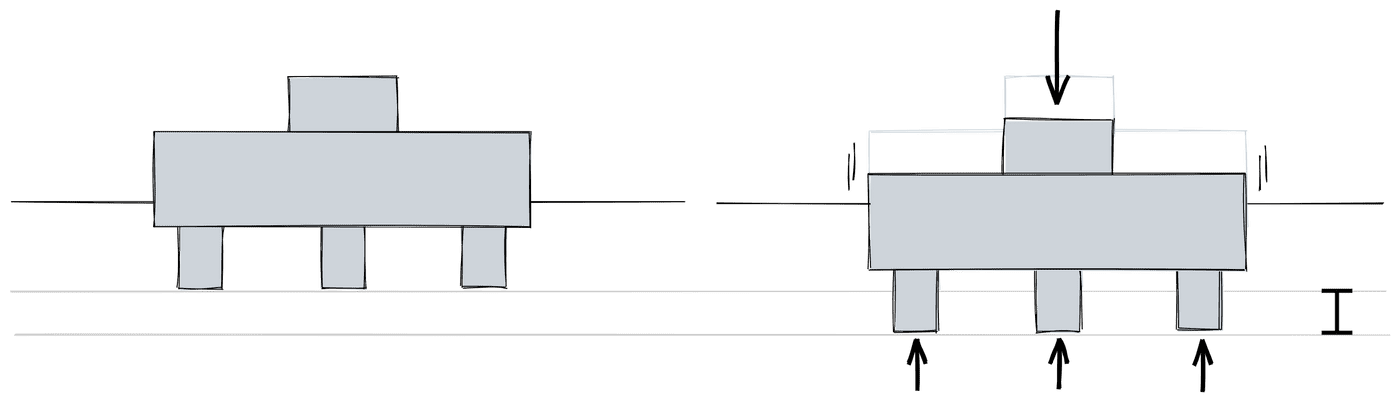
Como os deslocamentos de todas as estacas são iguais, então as reações também precisam ser.

Pelo equilíbrio de forças, a soma das reações precisa ser igual a força aplicada.

$F = \sum_{i=1}^{n_{estacas}} * R_i$

Como todas as reações são iguais:

$F = n_{estacas} * R_i$

Vamos interpretar o que essa equação diz. Ela diz que para calcular a reação em uma estaca, basta conhecer a força normal e a quantidade de estacas.

Apesar de intuitivo e até óbvio, é importante notar que essa equação não vale para blocos flexíveis. Nesse caso, não existe nenhuma garantia de que os deslocamentos são iguais e, portanto, não podemos simplesmente dividir a força aplicada pelo número de estacas.

Bloco de fundação rígido apenas com momento fletor

Vamos voltar ao exemplo da régua em um apoio mole e aplicar uma força na ponta.

Além de deslocar verticalmente, ela também rotaciona. Mas repare que ainda assim ela não se deforma e mantém a sua linha reta.

Quando existe apenas a força centrada, todos os deslocamentos verticais são iguais. Com um momento fletor, introduzimos uma parcela de rotação, de maneira que alguns pontos se deslocam mais na vertical do que outros.

No caso de um bloco rígido, se traçarmos uma reta ao longo do topo das estacas, essa reta apenas rotaciona após a aplicação do momento fletor, mas ainda assim é uma reta.

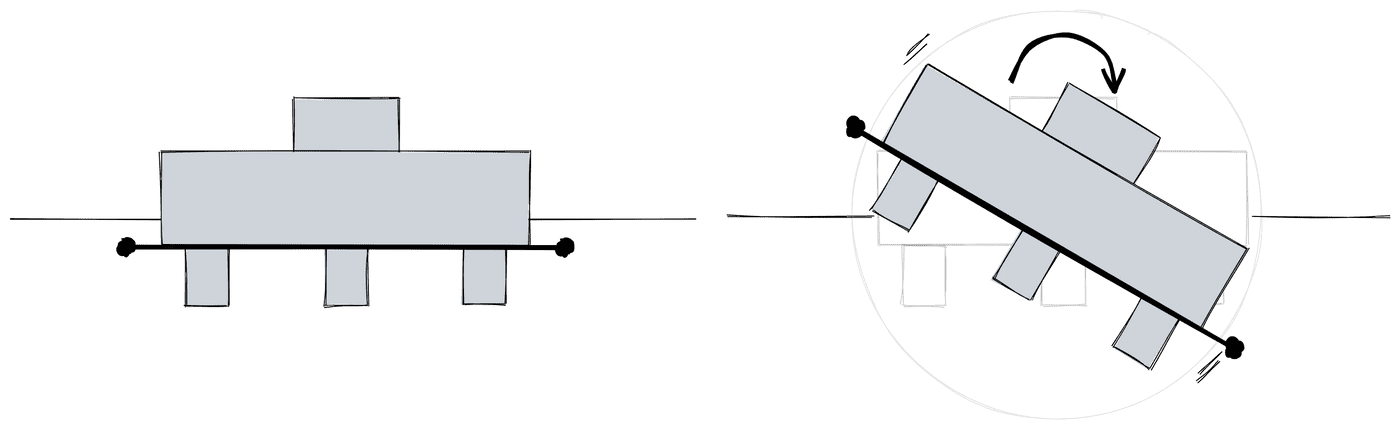
Como os pontos sobre as estacas descrevem uma reta, podemos utilizar a rotação do bloco para calcular o deslocamento vertical de cada estaca.

Apenas com uma simples equação de reta podemos equacionar o problema de calcular a reação da estaca quando aplicamos um momento fletor.

$y_i = x_i * tan(\theta)$ (Equação de reta)

$\theta$ = rotação do bloco

$R_i = y_i * k$ (Lei de Hooke)

$M_i = R_i * x_i$ (força * braço)

$M = \sum_{i=1}^{n_{estacas}} * M_i$ (equilíbrio)

As variáveis $\theta$ e $k$ são valores desconhecidos.

Fazendo um pouco de massagem 💆 nas equações, podemos chegar no seguinte:

Novamente, vamos interpretar esta equação. O que as variáveis $x_i$ e $\sum x^2$ nos dizem é que agora é necessário conhecer as posições de todas as estacas. Na situação apenas com força normal, bastava saber a quantidade de estacas. Agora, é preciso ter ideia de como as estacas estarão distribuídas no espaço.

Sobreposição de efeitos

As equações anteriores podem ser utilizadas quando temos apenas força normal ou apenas momento fletor. O último passo é expandi-las para serem utilizadas quando estes esforços estão presentes simultaneamente. Por sorte, esse processo é muito simples.

O conceito de sobreposição de efeitos diz que o efeito de duas ações aplicadas simultaneamente é igual a soma do efeito de cada ação aplicada isoladamente. Talvez em forma de equação fique mais claro:

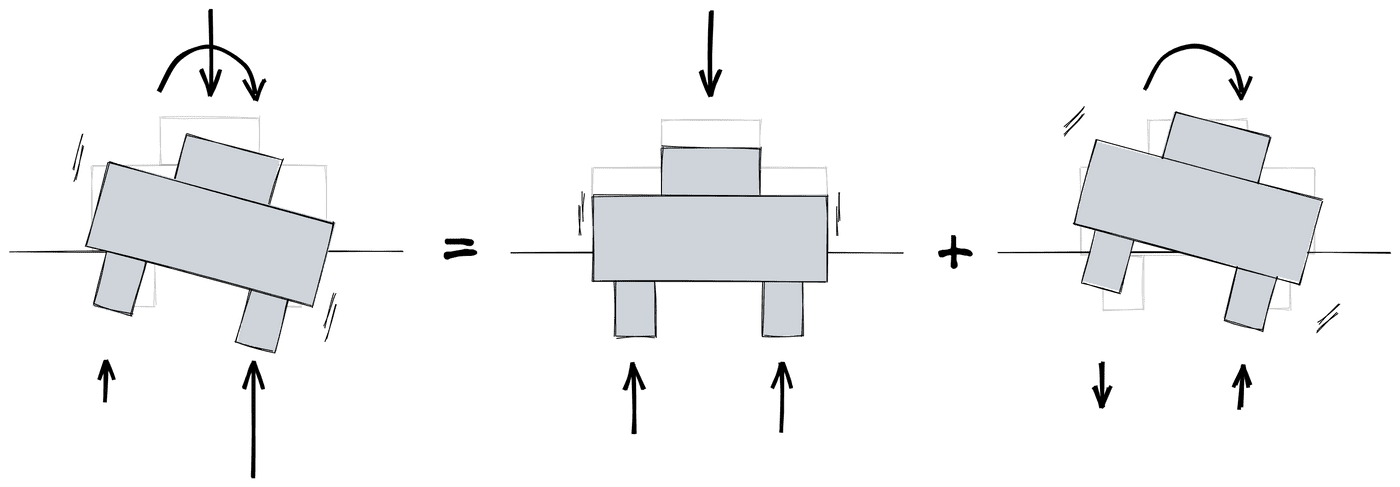
Sendo assim, a equação para calcular a reação com força normal e momento fletor é simplesmente a soma das duas equações:

Esse conceito também pode ser aplicado para quando temos momentos nas duas direções, basta somar o efeito dos momentos de cada direção:

E essa era a equação que eu queria chegar.

A primeira vez que tive contato com essa equação foi numa aula de pontes, quando é ensinado a distribuição de cargas na seção transversal. O famoso método de Engesser-Courbon. Quando aprendi sobre esse método, eu não tinha me ligado que ele também pode ser aplicado fora do contexto de pontes.

Próximos passos

Esta equação pode ser utilizada para calcular as reações de qualquer bloco rígido, inclusive quando temos mais de um pilar, neste caso, é necessário primeiro transportar as cargas para o centro de gravidade.

Este artigo foi bem teórico, mas achei importante ter o entendimento físico de bloco rígido na cabeça antes de entrar na parte mais prática.

No próximo artigo vamos aplicar estas equações e calcular as reações de alguns blocos.